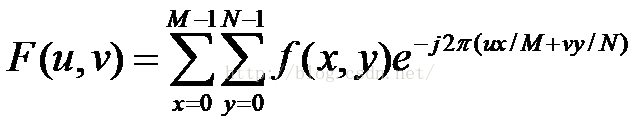本文共 878 字,大约阅读时间需要 2 分钟。
最近在看图像的傅里叶变换,看着频谱图一直没看明白到底为啥是那样的,跟同学研究了好久,终于想明白了。感谢同学的耐心指导!大家相互讨论真的很快就能出结果,多讨论,多学习。
图像的傅里叶变换
图像是一个二维的信号,所以对它进行二维的傅里叶变换,对于MXN的一幅图像的离散二维傅里叶变换,公式如下:
从公式上可以看出,F(u,v)与f(x,y)与并不是一一对应的关系,F(u,v)所对应的不是某一个f(x,y)而是所有的f(x,y)与e^(-j2TT(ux/M+vy/N))的乘积的和。
在冈萨雷斯书上看到类似如下图和它的频谱图,不理解它频谱图所代表的的意义。自己画了一幅类似的图,并用matlab试了一下。
用matlab做傅里叶变换(即用fft2()函数)之后的图如下:(这是一幅带相位的频谱图)
用matlab去掉相位之后的图像如下:
首先傅里叶变换就是将时域信号分解为不同频率的正弦函数(或余弦函数)之和,幅度表示该频率的正弦函数的个数。
可以看出四个角都是白色(255)表示占所有正弦函数的百分比大(幅度高)的低频部分,中间是黑色(0)表示占所有正弦函数的百分比小(幅度低)的高频部分
对其带相位的频谱图像中心化之后再去相位的图像如下:
这就是我们经常看见的傅里叶谱,也叫功率图,越亮代表能量越大,幅角越大。垂直方向与水平方向都有白色的条纹,说明在垂直方向与水平方向低频部分很明显。
(这个傅里叶变换之后的图像与夫朗和费矩形孔衍射图像一模一样,没有仔细研究过为什么)
以下是摘抄其他文章对图像傅里叶变化的理解,感觉很有用处。
图像的物理意义
如果只保留图像的中心点,则图像的细节会丢失,大致轮廓还在,不同区域好友不同的灰度。
如果保留远离中心的点,而去掉中心的幅度,则保留着图像的细节,而不同区域的灰度一样
这就得出了一个结论:傅里叶变换后的白色部分(即幅度较大的低频部分),表示的是图像中慢变化的特性,或者说是灰度变化缓慢的特性(低频部分)。
傅里叶变换后的黑色部分(即幅度低的高频部分),表示图像中快变化的特性,或者说是灰度变化快的特性(高频部分)。